ABC198 F - Cube

本番中にACはできなかったがかなりいいところまで行ったのでメモ。

問題はこちら↓

atcoder.jp

問題概要

立方体の各面に対して正の整数を定めたとき、その和がちょうど $S$ であるような決め方は何通りあるか、$998244353$ で割った余りを答えよ。ただし、回転して一致するようなもの同士は区別しない。

制約

• $6\leq S\leq 10^{18}$

バーンサイドの補題を使った解法

バーンサイドの補題（Burnside's lemma）という有名な群論の定理を使うと $O(1)$ で答えを求めることができる。

定理のステートメントは次の通り。

$G$ を位数 $n$ の群とする。要素数 $n$ の有限集合 $V$ の元に整数を割り当てる方法の個数は、$G$ の元による数の入れ替えによって一致するものを同一視すれば

$$ \frac{1}{|G|}\sum_{g\in G} |V^g| $$

に等しい。ここで $|V^g|$ は $g$ による入れ替えによって不変となるような整数の割り当て方の総数を表す。

※本当はもっと一般化できるのだが、問題を解くのに最低限必要な形で紹介した。証明は例えば http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/2016-16.pdf などに詳しい。

※競プロの文脈でよく登場する「ポリアの数え上げ定理」は、バーンサイドの補題を $G$ が対称群であるような場合に限定し拡張したものである。

定理の主張は堅苦しいが、要するに

• 回転などの操作によって一致するものを重複なく数える数え上げ問題は、その回転全体がなす群が既知の場合には楽に計算ができる

ということである。

今回の例で言えば、$G$ に相当するのは立方体の回転全体がなす群（正六面体群）である（実は $G\cong S_4$）。$G$ は $4!=24$ 個の元からなる。

バーンサイドの補題によれば、$G$ の $24$ 個の元 $g$ それぞれに対して、回転 $g$ を作用させたときに数の割り当てが変化しないような割り当て方の総数を求めればよい。

実際には、$24$ 通りを個別に考える必要はなく、性質の同じ元ごとにまとめて計算すればよい。実際、$24$ 種類の回転は性質の異なる以下 $5$ パターンに分類できる。

1. （恒等変換…$1$ 通り）恒等変換によって不変となるような数の書き込み方を数えるには、立方体の $6$ 個の面に書き込む数をすべて独立に決めてよい。
2. （面の中心を通る回転軸周りの $1/4$ 回転…$6$ 通り）この回転を行っても不変になるためには、独立に決めてよい数は $3$ 個だけで、同じ数を $1, 1, 4$ 個ずつ書き込む必要がある。
3. （面の中心を通る回転軸周りの $1/2$ 回転…$3$ 通り）この回転を行っても不変になるためには、独立に決めてよい数は $4$ 個だけで、同じ数を $1, 1, 2, 2$ 個ずつ書き込む必要がある。
4. （立方体の中心を通る対角線周りの $1/3$ 回転）独立に決めてよい数は $2$ 個だけで、同じ数を $3, 3$ 個ずつ書き込む必要がある。
5. （辺の中点を通る回転軸周りの $1/2$ 回転…$6$ 通り）独立に決めてよい数は $3$ 個だけで、同じ数を $2, 2$ 個ずつ書き込む必要がある。

ここから先は高校数学だけで求めることができる。結局、

• $a_1+\cdots+a_6=S$ の自然数解の個数を $A$
• $a_1+a_2+4a_3=S$ の自然数解の個数を $B$
• $a_1+a_2+2a_3+2a_4=S$ の自然数解の個数を $C$
• $3a_1+3a_2=S$ の自然数解の個数を $D$
• $2a_1+2a_2+2a_3=S$ の自然数解の個数を $E$

としたとき

$$ \frac{1}{24}(A+6B+3C+8D+6E) $$

が答えになることがわかる。あとは $A,B,C,D,E$ が求まればよい。

$a_1+\cdots+a_6=S$ の自然数解の個数

これは数学Aでおなじみの典型問題で、その答えは$S-6$ 個のマルと $5$ 個の仕切り棒を並べる順列の総数に等しい。よって

$$ A={}_{S-1}{\rm C}_5=\frac{1}{5!}(S-1)(S-2)(S-3)(S-4)(S-5). $$

$a_1+a_2+4a_3=S$ の自然数解の個数

$a_3$ を固定すれば、その答えは$S-4a_3-2$ 個のマルと $1$ 個の仕切り棒を並べる順列の総数に等しい。よって

$$ B=\sum_{k=1}^{\lfloor \frac{S-2}{4} \rfloor} (S-4k-1)=T(S-2T-3) $$

である（$T=\lfloor (S-2)/4\rfloor$ とおいた）。

$a_1+a_2+2a_3+2a_4=S$ の自然数解の個数

$a_3, a_4$ を固定すれば、その答えは$S-2a_3-2a_4-2$ 個のマルと $1$ 個の仕切り棒を並べる順列の総数に等しい。よって

$$ \begin{align} C&=\sum_{i, j}^{4\leq 2i+2j\leq S-2} (S-2i-2j-1)\\ &=\sum_{k=2}^{\lfloor \frac{S-2}{2} \rfloor}(S-2k-1)(k - 1)\\ &=\frac{1}{6}U(U-1)(3S-4U-7) \end{align} $$

である（$U=\lfloor (S-2)/2\rfloor$ とおいた）。

$3a_1+3a_2=S$ の自然数解の個数

これは簡単で、$S$ が $3$ の倍数でないなら答えは $0$、そうでなければ

$$ D=\frac{S}{3}-1 $$

である。

$2a_1+2a_2+2a_3=S$ の自然数解の個数

これも簡単で、$S$ が $2$ の倍数でないなら答えは $0$、そうでなければ

$$ E={}_{S/2-1}{\rm C}_2=\frac{1}{2}(S/2-1)(S/2-2) $$

である。

結論

以上より、$A, B, C, D, E$ が $O(1)$ で計算できるので、全体として $O(1)$ で答えを求めることができる。

自分の提出

ごちゃごちゃしていますが悪しからず…。

Submission #21701170 - AtCoder Beginner Contest 198

おいしいサンドイッチの作り方（前編）

みなさんお久しぶりです。

今日は、「サンドイッチ問題」「ピザサンドイッチの問題」「うどんピザサンド問題」などと呼ばれる数学の問題について得られた知見をまとめていこうと思います。

「サンドイッチ問題」は、2019年12月に「数学デー」*1というイベントで生まれた問題です。そのイベントに参加した友人から話を聞いて興味を持った私が、友人の助けを借りてあれこれ考えてみたところ、思いのほか強力な結果が得られ「サンドイッチ問題」をほとんど解決することができました。その結果を限られた人たちの間に留めておくのはもったいないと思い、ネットの海に放流することを決意した次第です*2。

数学デー史上最も実りのない話題だと思われていた（俺が思ってただけ）ピザの話、めちゃくちゃ進捗でた#数学デー#数学デーinN高 pic.twitter.com/0X5IBflW4Q

— 鯵坂もっちょ🐟 (@motcho_tw) January 10, 2020

前提知識

サンドイッチ問題を説明するために、まずは用語や概念の定義を行います。

ピザとサンドイッチ

ピザ

これをピザ（pizza）といいます。ピザはピザでも抽象的なピザで、具がのっている面（A面）と具がのっていない面（B面）があることが重要です。その他の特徴（マルゲリータかどうか、etc...）は捨象することにします。

ピザを複数枚重ねると、ピザの塔ができます。

ピザとサンドイッチ

これをサンドイッチ（sandwich）*3と呼ぶことにします。

同じ枚数のピザからなるサンドイッチであっても、面どうしがどのように重なっているかによって複数種類のサンドイッチが存在することに注意しましょう。例えば、以下のサンドイッチはすべて異なります*4。

異なる3つのサンドイッチ

ピザが何枚も重なった絵をいちいち書くわけにはいかないので、サンドイッチを表す便利な表記法を導入します。A面を表にしているピザを「$>$」、B面を表にしているピザを「$<$」に対応させ、上から「ABBA」のように重なっているサンドイッチを$><<>$と表記することにします*5。不等号の開いている側に具がのっているイメージです。例えば、「$<>$」は具が載っている面どうしが向かい合わせにくっついているような（まともな）サンドイッチです。

以上の話を厳密に書くと下のようになります。

（サンドイッチ）

集合 $P=\{<, >\}$ の元をピザといい、$n$ 枚のピザからなる順序組 $(p_1,\cdots, p_n)\;(p_i\in P)$ をサンドイッチという。

このとき、次の事実が成り立ちます。

（サンドイッチの個数）

$n$ 枚のピザからなるサンドイッチは $2^n$ 通り存在する。

これは、サンドイッチを構成する $n$ 枚のピザそれぞれに対して $<, >$ の $2$ 通りの選択肢が存在することから分かります。

grabbableなサンドイッチ

サンドイッチの中でも、1枚目のピザが $<$ で最後のピザが $>$ であるようなものを grabbableなサンドイッチ*6と呼ぶことにします。

grabbableなサンドイッチ（イメージ図）

例えば、$<<>>>$ はgrabbableですが、$><<<>$ はそうではありません。サンドイッチの両端を掴んだときに具が剥き出しになっておらず、手を汚さないサンドイッチがgrababbleです。明らかに、以下の命題が成り立ちます。

grababbleなサンドイッチをひっくり返したものもgrabbableである。

せっかくなので、「ひっくり返す」に相当する記法を用意しましょう。サンドイッチ $s=(p_1,\cdots, p_n)$ に対して、$s$ をひっくり返したサンドイッチを $s^{\rm T}:=(p_n^{\rm T}, \cdots, p_1^{\rm T})$ で表すことにします（ただし$(>)^{\rm T}=<, (>)^{\rm T}=<$）。例えば $(<<>)^{\rm T}=<>>$ です。

ピザ $n$ 枚からなるgrababbleなサンドイッチは、最初と最後の1枚ずつが確定していますから、次の事実が成り立ちます。

（grabbableなサンドイッチの個数）

$n$ 枚のピザからなるgrababbleなサンドイッチは $2^{n-2}$ 通り存在する。

サンドイッチ問題

これでサンドイッチ問題を説明する準備が整いました。

$n\;(\geq 2)$ 枚のピザを使い、以下の操作を行ってgrabbableなサンドイッチをつくることを考えます。

操作

1. はじめ、$n$ 枚のピザが具が載っている面を上にして（$>$ の状態で）横一列に並んでいる。
2. 隣り合う $2$ つのサンドイッチを任意に選び、左側のサンドイッチをひっくり返して右側のサンドイッチに重ねる。
3. 2. を$n-1$ 回繰り返し、$n$ 枚のピザからなるgrabbableなサンドイッチをつくる*7。

例えば、以下のように「操作」を行うと $3$ 枚のピザからなるサンドイッチを作ることができます。

サンドイッチを生成する「操作」

最終的に $<>>$ というサンドイッチができていることが分かりますね。

さて、このような「操作」を考えたとき、以下のような疑問が湧いてきます。これがサンドイッチ問題です。

サンドイッチ問題

1. この「操作」によって、どんなgrabbableサンドイッチも作ることができるのだろうか？
2. 同じgrabbableサンドイッチを生成するという同値関係によって「操作」を分類したとき、その完全代表系を構成できるか？
3. あるgrabbableサンドイッチを生成するような「操作」は何種類存在するか？

問題1.のモチベーションは理解しやすいでしょう。grabbableサンドイッチの完成形が与えられたとき、それを生成するような「操作」は必ず存在するでしょうか？もしかしたら、どのように「操作」を行っても生成することができないようなgrabbableサンドイッチが存在するかもしれません。

問題2., 3. が生まれた理由は次のようなものです。実は、異なる「操作」を行ったにもかかわらず、最終的に生成されるサンドイッチが同じである場合が存在します。すなわち、あるgrabbableサンドイッチを生成する「操作」が複数存在することがあるのです。どういったサンドイッチに複数通りの「操作」が存在して、どういったサンドイッチには1通りしか存在しないのでしょうか？その構造が知りたくなります。

こういう時の常套手段として、「操作」を同じサンドイッチを生成するものごとにグループ化することがよくあります。

操作をグループ化する

上のように「操作」をグループ分けして分類したとき、次のことが達成できれば、この「操作」のことがだいたい分かったと言えそうです。

• グループごとに代表選手を選ぶことができ、その代表の共通点が分かっている。（＝各サンドイッチを生成するような重複のない「レシピ集」を作ることができる）
• 各グループの構成人数を求める方法が分かっている。（＝サンドイッチが与えられたときに、そのサンドイッチを生成する「操作」の個数を求めることができる）

この$2$つが達成可能かを問うているのが、問題2.と問題3.であるというわけです。

問題1（任意のgrabbableサンドイッチが生成可能か？）

結論から言うと、問題1の答えはYESです。以下の事実が成り立ちます。

（任意のgrabbableサンドイッチは生成可能）

$n$ 枚からなる任意のgrabbableサンドイッチ $s$ に対して、$s$ を生成するような「操作」が存在する。

証明のポイントは、「操作を逆向きに見る」ことです*8。完成形から、1つ手前のステップ、2つ手前のステップ…と遡っていくことで、最終的に初期状態にすることができれば、証明が完了します。

ここで、次の事実に注目します。

• 「操作」の途中に現れるサンドイッチはすべて、grabbableであるか、$>$ である。

これを念頭におくと、任意のgrabbableサンドイッチ $s$ に対して、1ステップ前の状態を構成することができることが分かります。実際、

1. $s=<<\cdots >$ という形をしているならば、1ステップ前の状態として $>\;+\;<\cdots >$ がとれる（$<\cdots >$ はgrabbable）。
2. $s=<\cdots >>$ という形をしているならば、1ステップ前の状態として $(<\cdots >)^{\rm T}\;+\; >$ がとれる（$(<\cdots >)^{\rm T}$ はgrabbable）。
3. それ以外の場合は、必ず $s=<\cdots ><\cdots >$の形をしている*9ので、1ステップ前の状態として $(<\cdots >)^{\rm T}\;+\; <\cdots >$ がとれる。

が成り立つので、任意のgrabbableサンドイッチ $s$ に対して、1ステップ前の状態が構成できました。これを繰り返し用いれば、最終的に初期状態まで遡ることができます。

1ステップ前の状態を構成する

したがって、この「操作」によって任意のgrabbableサンドイッチが生成可能であることが分かりました。

次回予告

長くなってしまったので記事を分けることにします。問題2と問題3の答え（非常にボリュームが多いです）は次回の記事で説明したいと思います。お楽しみに。

*1:数学好きの人々が都内で集まってゆるーく数学の話をするイベントです。Twitter (@sugaku_day)を見ると感じがつかめると思います。ちなみに筆者は行ったことがありません。

*2:もうすぐ年末ですし。

*3:ピザタワーと呼ぶ流儀もあります。

*4:①と③はひっくり返すと同じになりますが、異なるサンドイッチであると定義することにします。

*5:本質的には括弧列なので、$)(()$と書いてもよかったのですが、すでにこの表記が一部界隈で定着しているようなのでそのままにしました。

*6:和訳するなら「可把（かは）」あるいは「可握（かあく）」でしょうか。

*7:この操作をどのように行っても、最終的にできるサンドイッチはgrabbableになることが証明できます。

*8:競技プログラミングなどでも頻出の考え方ですね。

*9:1.,2.に該当しないならば、$s$がどのような形をしていても、必ず $>$ と $<$ の境目が存在するからです。

二項係数にからんだ数列の極限を考えようとしたら闇が深かった話（後編）

ごめん、同級会には行けません。

いま、ロシアにいます。

というわけで、大学の研修でロシア第2の都市サンクトペテルブルクに来ています。いま起きたところなのですが、朝8時まで寝てようと思ったら朝5時に目が覚めてしまい、特にすることもないので、ブログ記事を書いている次第でございます。

さて、この記事は前回の続きになっておりますので、まだ前編を読んでない人は下のリンクから記事にとんでください。

halphy.hatenablog.com

念のため、忙しい人のために前回のあらすじをざっくり説明しますね。

次のような数列の$n\to\infty$でのふるまいを求めようとしていたのでした。

$$ a_n=\sum_{k=0}^n {}_n{\rm C}_k k^n $$

そして、OEIS（オンライン整数列大辞典）の記事に、このような記述を見つけ、なんとかしてこれを証明してやろうということになったのでした。

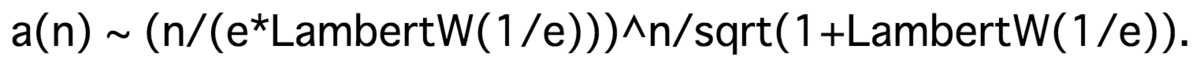
この式、何度見てもやばい香りがします。筑波山か富士山かでいったら富士山級です。 ちなみに、みなさんは日本で２番目に高い山を知っていますか？ 僕は知ってます。北岳です。３番目は知りません。

もう一回さっきの式を書きますね。でーん。

$$ a_n=\sum_{k=0}^n {}_n{\rm C}_k k^n \sim \frac{1}{\sqrt{1+w}}\left(\frac{n}{ew}\right)^n $$

ここで$w$というのは$W(1/e)$のことで、$xe^x=1/e$を満たす実数$x$を意味します。値はおよそ$0.278$です。

さて、今からこれを証明していくわけですが、中高で合計6年間ぐらい数学を勉強してきたものの、「一般項がよくわからん数列の漸近挙動を調べる」方法を習ったことがありません。でも、だからといって簡単に諦めるのもなんだか悔しい。

こういうときは土台から固めていくのが大切です。もう一度、OEISの記事に戻ってみましょう。このページには、他にもたくさんのお役立ち情報が載っているはずです。その中で、使えそうなものを探せば、ゴールにたどりつけるはず。というわけで、記事をもう一度見直してみると……

まてよ……？

この式は何でしょう？ 唐突に

$$ \frac{1}{1+W(-xe^x)} $$

という関数が書かれているのが不思議ですし、何よりランベルトのW関数が含まれています。この式が、いったい何を意味しているのか、気になります！

実は、E.g.fというのは exponential generating function の略で、日本語では指数型母関数といいます。指数型母関数について説明する前に、そもそも母関数（generating function）とは何かについて書いておきましょう。

数列$\{a_n\}$があったとき、その数列の各項を係数にもつべき級数

$$ f(x)=\sum_{n=0}^{\infty} a_nx^n $$

のことを、$\{a_n\}$の母関数といいます。母関数にはさまざまなタイプがあり、

$$ g(x)=\sum_{n=0}^{\infty} \frac{a_n}{n!}x^n $$

という形で定義することもあります。こちらのほうは指数型母関数と呼びます。これに対し、よりオーソドックスな$f(x)$のほうを通常型母関数といいます。単に「母関数」と言ったときには通常型母関数のほうを指すことが多いです。

数列の母関数が分かっていれば、母関数をべき級数に展開することで数列の各項がわかります。逆に、数列の各項が分かっていれば、そこから母関数を構成することができます。そのため、数列と母関数は1対1に対応します。

というわけで、母関数は、数列のふるまいを解析する上で、かなり役立ってくれそうです。そこで、件の数列

$$ a_n=\sum_{k=0}^n {}_n{\rm C}_k k^n $$

の指数型母関数が

$$ \frac{1}{1+W(-xe^x)} $$

であることを証明すること、これを当面の目標としましょう。指数型母関数というのは、数列の各項を$n!$で割ったものを係数にもつべき級数のことだったので、今から証明する式は

$$ \frac{1}{1+W(-xe^x)}=\sum_{n=0}^{\infty} \left(\sum_{k=0}^n {}_n{\rm C}_k k^n\right)\frac{x^n}{n!} $$

です。

指数型母関数を求める証明

証明は2ステップに分かれています。

• Step 1 数列$n^n$の指数型母関数を求める。
• Step 2 それを利用して、例の数列の指数型母関数を求める。

それではやっていきましょう。make it possible with †ランベルトのW関数†

Step 1

まずは、準備として

$$ \frac{1}{1+W(-x)}=\sum_{n=0}^{\infty}\frac{n^n}{n!}x^n $$

という等式を証明しましょう。この式は、$\displaystyle{\frac{1}{1+W(-x)}}$という関数のべき級数展開の係数が$\displaystyle{\frac{n^n}{n!}}$になることを意味しています。つまり、関数$\displaystyle{\frac{1}{1+W(-x)}}$は数列$n^n$の指数型母関数になっているというわけです。

ちなみに、この等式はランベルトのW関数に関する文献を漁っていたら偶然見つけました^[1]。$n^n$という一見するとシンプルな数列の母関数が、$W(x)$という特殊関数を使わないと表せないというのはなんだか不思議な気がします。

証明をする前に、$\displaystyle{\frac{1}{1+W(-x)}}$のべき級数展開から本当に$n^n$が出てくるのか確かめておきましょう。今回もWolframAlphaにお世話になります。

検索バーにSeries[1/(1+ProductLog[-x]), {x,0,6}]と入力する*1と、関数$\displaystyle{\frac{1}{1+W(-x)}}$の$x=0$でのべき級数展開を、$x^6$の項まで表示してくれます。

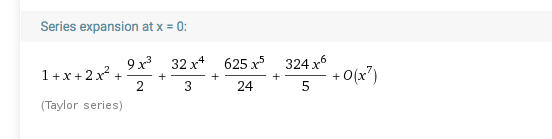
もしこの関数を指数型母関数にもつ数列が$n^n$なのであれば、級数展開の各項の係数を$n!$倍したものは$n^n$になるはずです。確かめましょう。

$n$	$x^n$の係数	$n!$	$x^n$の係数$\times n!$	$n^n$
$0$	$1$	$1$	$1$	$1$
$1$	$1$	$1$	$1$	$1$
$2$	$2$	$2$	$4$	$4$
$3$	$\displaystyle{\frac{9}{2}}$	$6$	$27$	$27$
$4$	$\displaystyle{\frac{32}{3}}$	$24$	$256$	$256$
$5$	$\displaystyle{\frac{625}{24}}$	$120$	$3125$	$3125$
$6$	$\displaystyle{\frac{324}{5}}$	$720$	$46656$	$46656$

表のいちばん右の2列を見てください。完全に一致しています。どうやら本当に

$$ \frac{1}{1+W(-x)}=\sum_{n=0}^{\infty}\frac{n^n}{n!}x^n $$

が成り立っていそうです。安心できたところで証明にうつりましょう。

証明で大活躍するのが、次のLagrange Inversion Theorem（Wikipedia英語版）という定理です。これは逆関数のべき級数展開を求めるときに有用な公式なのですが、その主張をラフに書くと以下のようになります*2。

Lagrange Inversion Theorem

関数$\varphi(y)$に対し、関係式$x=\displaystyle{\frac{y}{\varphi(y)}}$によって$x$から$y$への関数が定まるとする。このとき、

$$ \frac{1}{1-x\varphi'(y)}=\sum_{n=0}^{\infty}\frac{x^n}{n!}\left.\frac{d^n}{dy^n}(\varphi(y))^n\right|_{y=0} $$

が成り立つ。

ここで注意ですが、定理の主張はやや大雑把に書いており、細かい前提条件は省略しています。気になる人は専門の書物を読んでください。

定理の証明は文献[4]などを見ていただくとして、さっそくこの定理を利用してみましょう。そのためには、関数$\varphi(y)$の形を適切に決める必要がありますが、実は$\varphi(y)=e^y$とおくとうまくいきます。実際、$\varphi(y)=e^y$ならば$x$と$y$の関係は

$$ x=\frac{y}{e^y}=ye^{-y} $$

すなわち

$$ y=-W(-x) $$

です。一方、定理の式の左辺において$\varphi'(y)=(e^y)'=e^y$ですから

$$ \frac{1}{1-x\varphi'(y)}=\frac{1}{1-xe^y}=\frac{1}{1-y}=\frac{1}{1+W(-x)} $$

となり、うまく証明したい式の形を作ることができました。あとは、定理1の右辺である

$$ \sum_{n=0}^{\infty}\frac{x^n}{n!}\left.\frac{d^n}{dy^n}(\varphi(y))^n\right|_{y=0} $$

を計算してやるだけです。ここで問題なのは

$$ \left.\frac{d^n}{dy^n}(\varphi(y))^n\right|_{y=0}=\left.\frac{d^n}{dy^n}(e^y)^n\right|_{y=0}=\left.\frac{d^n}{dy^n}e^{ny}\right|_{y=0} $$

の部分ですが、これは「関数$e^{ny}$の$y=0$での$n$階微分係数」という意味なので、関数$e^{ny}$を繰り返し微分してそこに$y=0$を代入すればよいですね。計算してみると分かりますがその値は$n^n$になります。というわけで、証明したかった式である

$$ \frac{1}{1+W(-x)}=\sum_{n=0}^{\infty}\frac{n^n}{n!}x^n $$

が導出できました。やったぜ。

というわけで、Step 1の定理はLagrange Inversion Theoremという強力な定理を利用することで証明できました。ちなみに、この定理は複素解析*3の手法を用いた証明が知られているそうです。

Step 2

次はStep 2です。Step 2は証明がやや長い上にそこそこ複雑なので、結果だけ見たい人は次にとんでください。

さて、ここでは、先ほど証明した

$$ \frac{1}{1+W(-x)}=\sum_{n=0}^{\infty}\frac{n^n}{n!}x^n $$

から

$$ \frac{1}{1+W(-xe^x)}=\sum_{n=0}^{\infty} \left(\sum_{k=0}^n {}_n{\rm C}_k k^n\right)\frac{x^n}{n!} $$

を導きます。2つの式をじっと見比べると、1つ目の式において$x\to xe^x$という置き換えを行なうと2つ目の式になることに気づきます*4。ということは、1つ目の式の$x$を$xe^x$に置き換えた式を考えればよさそうです。やってみましょう。

$$ \frac{1}{1+W(-xe^x)}=\sum_{n=0}^{\infty}\frac{n^n}{n!}(xe^x)^n $$

ここで行き詰まりそうになりますが、$xe^x$という関数もべき級数で書くことができるので、それを利用しましょう。$e^x$のべき級数展開を覚えている人は多いと思うので*5、それを$x$倍するだけです。

$$ xe^x=x\sum_{n=0}^{\infty} \frac{x^n}{n!}=\sum_{n=1}^{\infty} \frac{x^n}{(n-1)!}=\sum_{n=1}^{\infty} \frac{n}{n!}x^n $$

これを先ほどの式に代入します。どーん。

$$ \frac{1}{1+W(-xe^x)}=\sum_{n=0}^{\infty}\frac{n^n}{n!}\left(\sum_{m=1}^{\infty} \frac{m}{m!}x^m\right)^n $$

いきなりという文字が登場しても戸惑わないでくださいね。シグマ記号で使うダミー変数は何でもいいのですが、内側のシグマ記号で$n$を使ってしまうと外側のシグマ記号のダミー変数$n$と被ってしまうので仕方なくにしただけです。

さてこの式。無限和の中に無限和があって、見た目の醸し出すオーラが半端じゃない。どうにかしてこれを簡単にしたいです。 問題なのは$\displaystyle{\left(\sum_{m=1}^{\infty} \frac{m}{m!}x^m\right)^n}$の部分です。よく見ると、無限個の項の和の$n$乗になっていて、これを展開するのは少し厄介な気がします。

とはいえ、ゆっくり考えればそれほど怖くはありません。いま知りたいのは、関数$\displaystyle{\frac{1}{1+W(-xe^x)}}$のべき級数展開の各項の係数です。では、例えば$x^N$の係数を知りたいときどうすればよいでしょう？

答えは単純です。二重シグマの式を展開した結果が$x^N$になるような項を、ひとつ残らず拾い集めればよいのです。

ここから先の話はいささか抽象的なので、その前に具体的な値で感覚をつかみましょう。例えば$N=2$としてみましょう。関数$\displaystyle{\frac{1}{1+W(-xe^x)}}$のべき級数展開の$x^2$の項の係数はいくつになるでしょうか。式を展開した結果が$x^2$になるような項をすべてかき集めてみましょう。

まず、外側のシグマ記号を考えます。$n=0,1,2,\cdots$のそれぞれに対して、$x^2$の項がどこに現れるかを探してみましょう。

$n=0$のとき、シグマの中身は$1$ですから、これが$x^2$の項を生み出すことはありません。

次に$n=1$のとき、シグマの中身は

$$ \left(\sum_{m=1}^{\infty} \frac{m}{m!}x^m\right) $$

になりますから、$x^2$の項は、このうち$m=2$に対応する項に現れます。つまり、$n=1$のときの和から

$$ \frac{2}{2!}x^2=x^2 $$

という項が現れることが分かります。

さらに$n=2$のときを調べましょう。シグマの中身は

$$ \frac{2^2}{2!}\left(\sum_{m=1}^{\infty} \frac{m}{m!}x^m\right)^2=2\left(\sum_{m=1}^{\infty} \frac{m}{m!}x^m\right)\left(\sum_{m=1}^{\infty} \frac{m}{m!}x^m\right) $$

という2つの無限和の掛け算になっています。よって、ここから$x^2$の項が出てくるのは、

• 1番目の和で1次の項を選び、2番目の和で1次の項を選んだとき

です。したがって、$n=2$のときの和からは

$$ 2\cdot \frac{1}{1!}x\cdot \frac{1}{1!}x=2x^2 $$

という項が現れることが分かります。

最後に$n=3$以降ですが、最低でも次数が$3$の項しか現れないので、ここから$x^2$の項が出てくることはありません。

というわけで、$x^2$の項は

$$ x^2+2x^2=3x^2 $$

になることが分かりました。

具体的な例で仕組みが分かったところで、今までの話を一般化しましょう。$x^N$の係数を求めるために、$n=1,2,\cdots, k,\cdots, N$のそれぞれについて、$x^N$が現れる項を探します。

一般に、$n=k$のときを考えましょう。シグマ記号の中身は

$$ \frac{k^k}{k!}\left(\sum_{m=1}^{\infty} \frac{m}{m!}x^m\right)^k $$

ですから、あとは$\displaystyle{\left(\sum_{m=1}^{\infty} \frac{m}{m!}x^m\right)^k}$を展開したときに、$x^N$が現れるような項の選び方を考えます。

さて、$\displaystyle{\left(\sum_{m=1}^{\infty} \frac{m}{m!}x^m\right)^k}$というのは

$$ \left(\sum_{m=1}^{\infty} \frac{m}{m!}x^m\right)\cdot \left(\sum_{m=1}^{\infty} \frac{m}{m!}x^m\right)\cdots \left(\sum_{m=1}^{\infty} \frac{m}{m!}x^m\right) $$

という$k$個の無限次多項式の積です。それぞれの因数からどの項を選べばよいか考えましょう。掛け算は順序によらないので、何次の項を何個選んでくるかのみが重要です。そこで、$x$の項を$p_1$個、$x^2$の項を$p_2$個、…、$x^{N-k+1}$の項を$p_{N-k+1}$個選んだとします*6。項は合計$k$個あるので、もちろん

$$ p_1+p_2+\cdots+p_{N-k+1}=k \tag{*} $$

です。これを満たすように$p_1, p_2,\cdots,p_{N-k+1}$を選んだとき、掛け算した結果ちょうど次数が$N$になる（$x^N$の項になる）ためには、さらに

$$ p_1+2p_2+\cdots+(N-k+1)p_{N-k+1}=N \tag{**} $$

が成り立っている必要があります。

逆に言えば、(*)かつ(**)を満たすような負でない整数$p_1, p_2,\cdots,p_{N-k+1}$の組ならば、どんなものを選んできてもよいということです。

さらに、$p_1, p_2,\cdots,p_{N-k+1}$の組それぞれに対して、どの因子からどの次数の項をとってくるかで

$$ \frac{k!}{p_1!p_2!\cdots p_{N-k+1}!} $$

通りの場合があります。いきなりごつい式が登場して面食らうかもしれませんが、これは高校数学でおなじみの「同じものを含む順列」というやつです。$p_1$個の項、$p_2$個の項、…、$p_{N-k+1}$個の項の合計$p_1+p_2+\cdots+p_{N-k+1}=k$個を並べる順列の総数を求めるには、$k$個の項の順列を$p_1!p_2!\cdots p_{N-k+1}!$で割って同一視してやる必要がありますからね。

というわけで、$n=k$のときに現れる$x^N$の項の合計は

$$ \frac{k^k}{k!}\sum\frac{k!}{p_1!p_2!\cdots p_{N-k+1}!}\left(\frac{1\cdot x}{1!}\right)^{p_1}\left(\frac{2\cdot x^2}{2!}\right)^{p_2}\cdots \left(\frac{(N-k+1)x^{N-k+1}}{(N-k+1)!}\right)^{p_{N-k+1}} $$

と表すことができます。ここでシグマ記号に何も書かれていませんが、この式においては$p_1+p_2+\cdots+p_{N-k+1}=k$かつ$p_1+2p_2+\cdots+(N-k+1)p_{N-k+1}=N$を満たす非負整数$p_1, p_2,\cdots,p_{N-k+1}$すべてにわたる和を考えることと約束します。

あとは、$n=1,2,\cdots, k,\cdots, N$について、$x^N$が現れる項をすべて足してやれば、それが求めたかった$x^N$の項の合計になっています*7。

$$ \sum_{k=0}^N\frac{k^k}{k!}\sum\frac{k!}{p_1!p_2!\cdots p_{N-k+1}!}\left(\frac{1\cdot x}{1!}\right)^{p_1}\left(\frac{2\cdot x^2}{2!}\right)^{p_2}\cdots \left(\frac{(N-k+1)x^{N-k+1}}{(N-k+1)!}\right)^{p_{N-k+1}} $$

見るからに複雑な式ができてしまい自分でもびっくりしています。あとはこれを頑張って変形していくのでしばしお付き合いください。見てるだけで疲れそうですね。

まずは$x$のべき乗を指数法則を使ってまとめていきます。また同時に、分子と分母に$k!$がいるので並行して約分してやります。

$$ \begin{eqnarray} &&\sum_{k=0}^N\frac{k^k}{k!}\sum\frac{k!}{p_1!p_2!\cdots p_{N-k+1}!}\left(\frac{1\cdot x}{1!}\right)^{p_1}\left(\frac{2\cdot x^2}{2!}\right)^{p_2}\cdots \left(\frac{(N-k+1)x^{N-k+1}}{(N-k+1)!}\right)^{p_{n-k+1}}\\ &=&\sum_{k=0}^Nk^k\sum\frac{1}{p_1!p_2!\cdots p_{N-k+1}!}\left(\frac{1}{1!}\right)^{p_1}\left(\frac{2}{2!}\right)^{p_2}\cdots \left(\frac{(N-k+1)}{(N-k+1)!}\right)^{p_{N-k+1}}x^{p_1+2p_2+\cdots+(N-k+1)p_{N-k+1}}\\ &=&\sum_{k=0}^Nk^k\sum\frac{1}{p_1!p_2!\cdots p_{N-k+1}!}\left(\frac{1}{1!}\right)^{p_1}\left(\frac{2}{2!}\right)^{p_2}\cdots \left(\frac{(N-k+1)}{(N-k+1)!}\right)^{p_{N-k+1}}x^N \end{eqnarray} $$

これ以上簡単にならなそうですが、実は、次のような等式を用いると、この式を格段にきれいにすることができます。

ベル多項式の特殊値

$p_1, p_2,\cdots,p_{N-k+1}$を$p_1+p_2+\cdots+p_{N-k+1}=k$かつ$p_1+2p_2+\cdots+(N-k+1)p_{N-k+1}=N$を満たす非負整数であるとするとき

$$ \sum\frac{N!}{p_1!p_2!\cdots p_{N-k+1}!}\left(\frac{1}{1!}\right)^{p_1}\left(\frac{2}{2!}\right)^{p_2}\cdots \left(\frac{(N-k+1)}{(N-k+1)!}\right)^{p_{N-k+1}}={}_N{\rm C}_k k^{N-k} $$

が成り立つ。

いきなり公式が天から降ってきた感じは否めませんがご容赦ください。この等式の証明の詳細は文献[5], [6]を見てもらうとして、ここでは証明の概略だけ紹介します。証明のステップは次の通りです。

1. 数列$\displaystyle{\sum_{k=0}^n{}_n{\rm C}_k k^{n-k}}$の指数型母関数が$\exp{(x\exp{x})}$であることを証明する*8。
2. 関数$\exp{(x\exp{x})}$のべき級数展開の各項に$\displaystyle{\sum_{k=0}^n\sum\frac{1}{p_1!p_2!\cdots p_{n-k+1}!}\left(\frac{1}{1!}\right)^{p_1}\left(\frac{2}{2!}\right)^{p_2}\cdots \left(\frac{(n-k+1)}{(n-k+1)!}\right)^{p_{n-k+1}}}$が現れることを証明する。

特に2.については、上の証明と全く同じ流れをたどるため、比較的理解しやすいでしょう。

この定理が成り立つことは認めれば、あとはもうゴールに向かって突き進むだけです。

$$ \begin{eqnarray} &&\sum_{k=0}^Nk^k\sum\frac{1}{p_1!p_2!\cdots p_{N-k+1}!}\left(\frac{1}{1!}\right)^{p_1}\left(\frac{2}{2!}\right)^{p_2}\cdots \left(\frac{(N-k+1)}{(N-k+1)!}\right)^{p_{N-k+1}}x^N\\ &=&\sum_{k=0}^N\frac{k^k}{N!}\sum\frac{N!}{p_1!p_2!\cdots p_{N-k+1}!}\left(\frac{1}{1!}\right)^{p_1}\left(\frac{2}{2!}\right)^{p_2}\cdots \left(\frac{(N-k+1)}{(N-k+1)!}\right)^{p_{N-k+1}}x^N\\ &=&\sum_{k=0}^N\frac{k^k}{N!}{}_N{\rm C}_k k^{N-k}\\ &=&\sum_{k=0}^N\frac{k^N}{N!}{}_N{\rm C}_k \end{eqnarray} $$

こんなにすっきりした式になりました。$\displaystyle{\sum_{k=0}^N\frac{k^N}{N!}{}_N{\rm C}_k}$というのはそもそも、関数$\displaystyle{\frac{1}{1+W(-xe^x)}}$のべき級数展開の$x^N$の係数を表していましたから、結局

$$ \frac{1}{1+W(-xe^x)}=\sum_{n=0}^{\infty} \left(\sum_{k=0}^n {}_n{\rm C}_k k^n\right)\frac{x^n}{n!} $$

が証明できたことになります。すなわち、例の数列$\displaystyle{\sum_{k=0}^n {}_n{\rm C}_k k^n}$の指数型母関数が$\displaystyle{\frac{1}{1+W(-xe^x)}}$という関数であることが分かりました。

結果を噛みしめる

ふー。さすがに疲れましたね。とはいえ、いま証明した内容を見直してみると、なかなか興味深いことを言っていることが分かります。数列の一般項は和の形でしか表せないのに、その母関数の形はきっちり分かってしまうんです。結構すごくないですか。

さて、せっかく指数型母関数が$\displaystyle{\frac{1}{1+W(-xe^x)}}$であることが分かったので、実際に$\displaystyle{\frac{1}{1+W(-xe^x)}}$の級数展開を求めることで例の数列の各項を求めてみましょう。今回使用するのはやっぱりWolframAlphaくんです。なんだかWolfram Research社の回し者みたいになってきました。スポンサーについてくれないかなあ()

検索窓にSeries[1/(1+ProductLog[-xe^x]), {x,0,6}]と入力して、数列の第$6$項までを求めてやりましょう。

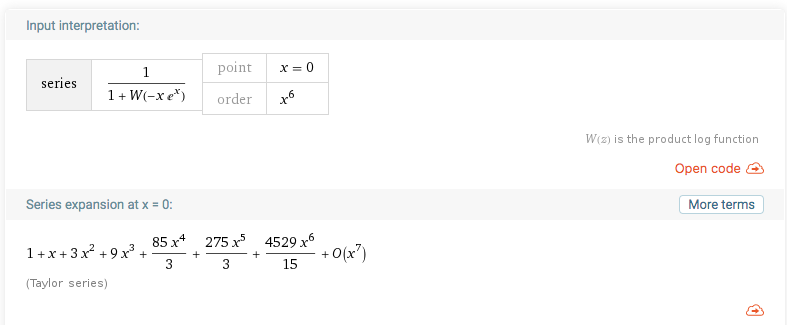
級数展開の各項の係数を$n!$倍すれば、それが$\displaystyle{\sum_{k=0}^n {}_n{\rm C}_k k^n}$になっているはずです。はたしてそうなっているでしょうか。

$n$	$x^n$の係数	$n!$	$x^n$の係数$\times n!$
$0$	$1$	$1$	$1$
$1$	$1$	$1$	$1$
$2$	$3$	$2$	$6$
$3$	$9$	$6$	$54$
$4$	$\displaystyle{\frac{85}{3}}$	$24$	$680$
$5$	$\displaystyle{\frac{275}{3}}$	$120$	$11000$
$6$	$\displaystyle{\frac{4529}{15}}$	$720$	$217392$

$1,1,6,54,680,11000,217392,\cdots$これは紛れもなくあの数列です。達成感ありますね。

母関数がわかれば漸近挙動がわかる

いやちょっと待って。なんか終わった気になっていませんか？ 母関数を求めただけで満足しちゃってますよね？ まだ大事な仕事が残っています。そう、「例の数列の漸近挙動を求める」ためにこの記事を書いているんでした。

実は、例の数列の母関数を求めたことは、数列の漸近挙動を求めるための大事な準備になっているのです。なぜなら、「母関数が分かっていれば、それを利用して数列の漸近挙動を求めることができる」からです。

もう一度言いますよ。

「母関数が分かっていれば、それを利用して数列の漸近挙動を求めることができる」んです。

信じられない？ ほんとです。Wikipediaもそう言っています()

ちょっとできそうな気がしてきましたね。

でも、どうやって？

この記述を見つけてからというもの、その方法を探し求めてネットの海を彷徨いましたが、一向に見つかりません。情報が結構ありそうなトピックなのに、探してみると意外にないものです。

ようやく文献を見つけたときには、探し始めてから2日が経っていました。

"Analytic Combinatorics"とかいう本が神

その文献というのがこちらです。

Analytic Combinatorics

"Analytic Combinatorics"（直訳すると「解析的組合せ論」）は、解析学（微分積分学）の手法を用いて組合せ論の問題を解く方法について解説した824ページにわたる大著です。しかもなんとこの本、著者の方がWebページに全文を公開してくれています。なんて優しいんだ。というか採算とれてるのかな。

とにかく目次を見ると、「Part B: Complex Asymtotics」という部分に、数列の漸近挙動を解析する話が述べられているようなのですが、なんとその説明に400ページ弱も費やされています。きっとそこに知りたい情報があるはず。さっそく読んでみました（流し読みですが）。

この本の言いたいことを要約すると

• 数列の漸近挙動は、母関数の特異点まわりのふるまいによって決まる

ということです。標語的に言っただけではよく分からないでしょうから、もう少し詳しく説明します。

いま、数列$\{f_n\}$の漸近挙動を知りたいとします。数列$\{f_n\}$の母関数$f(x)$をがんばって発見したとしましょう。この関数$f(x)$は$x=a$という点を（発散するなどして）特異点に持つとします。このとき、$x$を$a$に近づけたときの発散（or収束）の仕方、すなわち$x\to a$での漸近挙動が$f(x)$と同じであるような標準的な関数$g(x)$が存在して、しかも$g(x)$を母関数にもつ数列$\{g_n\}$の漸近挙動が既知ならば、もとの数列$\{f_n\}$の漸近挙動を知ることができます。なぜなら、数列$\{f_n\}$の漸近挙動は数列$\{g_n\}$の漸近挙動と実は同じになるからです。

これを今回の話に当てはめると、つまりこういうことです。いま、

$$ f_n=\sum_{k=0}^n {}_n{\rm C}_k k^n $$

という数列の漸近挙動を求めようとしています。僕たちは、この数列$\{f_n\}$の（指数型）母関数$f(x)$が

$$ f(x)=\frac{1}{1+W(-xe^x)} $$

であることを知っています。この関数は、分母が$0$になるときがあるため特異点を持ちます。そのときの$x$の値を求めておきましょう。$1+W(-xe^x)=0$となるような$x$は

$$ -xe^x=-\frac{1}{e} $$

すなわち

$$ x=W\left(\frac{1}{e}\right)(=w) $$

です。さて、いまからやることは、$x\to w$での漸近挙動が$f(x)$と同じになるような$g(x)$をなんとかして発見することです。式で書けば

$$ f(x)\sim g(x) \; (x\to w) $$

となります。記号「$\sim$」は数列の$n\to \infty$の極限を考えるときにしか定義していませんでしたが、それを拡張して、関数については

$$ \lim_{x\to w}\frac{f(x)}{g(x)}=1 $$

が成り立つとき$f(x)\sim g(x) \; (x\to w)$と表す、と約束します。

ところで、$g(x)$は何でもいいわけではありません。$g(x)$は、これを母関数にもつ数列の漸近挙動が既知であるような、そういう標準的な関数である必要があります。もし運良くそのような$g(x)$を発見できれば、$g(x)$を母関数にもつ数列の漸近挙動を求めることで、もとの数列$\{f_n\}$の漸近挙動を知ることができるというわけです。めでたしめでたし。

まずは練習

いま説明したことをいきなり$\displaystyle{\frac{1}{1+W(-xe^x)}}$でやるのは荷が重いので、その前にもっと簡単な例で感覚をつかみましょう。まずは$f_n=n^n$を例にとり、

$$ f(x)=\frac{1}{1+W(-x)} $$

を調べてみます。この関数は、分母が$0$になる点をもちます。そのような点の$x$座標を求めるには、$1+W(-x)=0$を解けばよいので、最終的に

$$ x=\frac{1}{e} $$

を得ます。すなわち、この関数は$x=1/e$を特異点にもつことが分かりました。そこで、

$$ \frac{1}{1+W(-x)}\sim g(x) \; \left(x\to \frac{1}{e}\right) $$

となるような標準的な関数$g(x)$を探しましょう。ここからの計算は、大部分を"Analytic Combinatorics"のp.403（Example VI.8）に依拠しています。適宜参考にしてください。

さて、まず$y=-W(-x)$とおきます。すると、$x$と$y$の関係は

$$ x=ye^{-y} $$

と表すことができます。ここで、両辺を$y$の関数とみなして$y=1$（$x=1/e$）のまわりでテイラー展開します。暗算でもできますが面倒くさいのでWolframAlphaにSeries[ye^(-y), {y, 1, 2}]と入力しましょう。

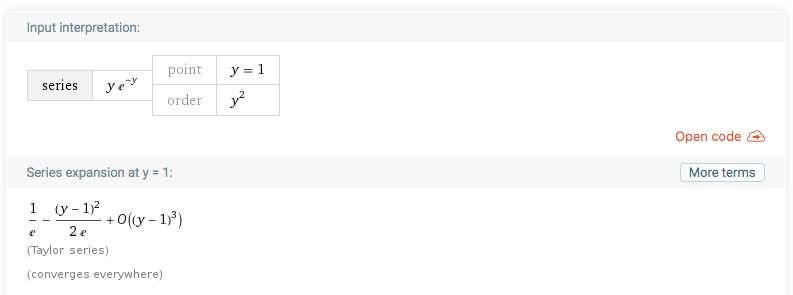
はい。2次の項で打ち切ると

$$ x=\frac{1}{e}-\frac{1}{2e}(y-1)^2+O( (y-1)^3) $$

となります（$O( (y-1)^3)$は誤差項を表します）。これを$y$についての2次方程式とみなし、解の公式を使って$y$について解いてみましょう。ただし、関数$ye^{-y}$の定義域が$y\leq 1$であることに注意してマイナスの符号を採用することに注意しましょう。結果はこうなります。

$$ y=1-\sqrt{2}\sqrt{1-ex}+O(1-ex) $$

ところで$y=-W(-x)$だったので

$$ 1+W(-x)=\sqrt{2}\sqrt{1-ex}+O(1-ex) $$

が成り立ちます。これは

$$ 1+W(-x)\sim\sqrt{2}\sqrt{1-ex} \; \left(x\to \frac{1}{e}\right) $$

を意味していますから、両辺の逆数をとれば

$$ \frac{1}{1+W(-x)}\sim\frac{1}{\sqrt{2}\sqrt{1-ex}} \; \left(x\to \frac{1}{e}\right) $$

がいえたことになります。というわけで、探していた関数

$$ g(x)=\frac{1}{\sqrt{2}\sqrt{1-ex}} $$

が見つかりました。あとは、$g(x)$を母関数にもつ数列の一般項を求めるだけです。

このまま計算してもいいのですが、いろいろ定数が入っていてごちゃごちゃしているので、まずは

$$ G(x)=\frac{1}{\sqrt{1-x}} $$

という、より標準的な関数を考えて、その結果を利用することにしましょう。そのほうが応用がききます。

$G(x)$を母関数にもつ数列を求めるためには、$G(x)$のべき級数展開を求める必要があります。そのために、$G(x)$の$n$階微分を計算しましょう。

$$ \begin{eqnarray} G(x)&=&(1-x)^{-\frac{1}{2}}\\ G'(x)&=&\frac{1}{2}(1-x)^{-\frac{3}{2}}\\ G''(x)&=&\frac{1}{2}\frac{3}{2}(1-x)^{-\frac{5}{2}}\\ G^{(n)}(x)&=&\frac{1}{2}\frac{3}{2}\cdots\frac{2n-1}{2}(1-x)^{-\frac{2n+1}{2}}\\ \end{eqnarray} $$

この計算から、$G(x)$の$x=0$での$n$階微分係数が

$$ G^{(n)}(0)=\frac{1}{2}\cdot\frac{3}{2}\cdots\left(n-\frac{1}{2}\right) $$

になることが分かりました。よって、$G(x)$のべき級数展開の$x^n$の項の係数$G_n$は

$$ G_n=\frac{1}{n!}\cdot\frac{1}{2}\cdot\frac{3}{2}\cdots\left(n-\frac{1}{2}\right) $$

になります。この式は、一般化二項係数*9を用いると

$$ G_n=\binom{n-1/2}{n} $$

と表すことができます。あとは、この数列の漸近挙動を求めるだけですが、実は

$$ \binom{n-1/2}{n}\sim \frac{1}{\sqrt{n}\Gamma(1/2)}=\frac{1}{\sqrt{\pi n}} \; (n\to\infty) $$

であることが知られています*10。ただし$\Gamma(x)$はかの有名なガンマ関数です。

したがって、

$$ G(x)=\frac{1}{\sqrt{1-x}} $$

という関数を母関数にもつ数列$G_n$の漸近挙動が

$$ G_n \sim \frac{1}{\sqrt{\pi n}} \; (n\to\infty) $$

であることが分かりました。さて、そもそもどうしてこんなことをしていたかというと

$$ g(x)=\frac{1}{\sqrt{2}\sqrt{1-ex}} $$

を母関数にもつ数列$g_n$の漸近挙動を知りたかったのでした。いま計算した結果をさっそく利用しましょう。母関数の定義より

$$ G(x)=\sum_{n=0}^{\infty} G_nx^n $$

ですが、ここで$x\to ex$という置き換えを行い、両辺を$1/\sqrt{2}$倍すれば、左辺は$g(x)$になって

$$ g(x)=\frac{1}{\sqrt{2}\sqrt{1-ex}}=\sum_{n=0}^{\infty} e^nG_nx^n $$

が成り立ちます。すなわち、$g(x)$を母関数にもつ数列$g_n$と、$G_n$の関係は

$$ g_n=e^nG_n $$

です。したがって、$g_n$の漸近挙動が

$$ g_n \sim \frac{e^n}{\sqrt{2\pi n}} \; (n\to\infty) $$

になることが分かりました。そもそも$n!g_n$は、数列$n^n$と同じように漸近する数列だった*11のですから、最終的に

$$ n^n \sim \frac{n! e^n}{\sqrt{2\pi n}} \; (n\to\infty) $$

がいえたことになります。

ここでやったことを簡単にまとめておきましょう。

1. 数列$f_n=n^n$の漸近挙動を調べるため、$f_n$の指数型母関数が$f(x)=\displaystyle{\frac{1}{1+W(-x)}}$であることを求めた。
2. $f(x)$は$x=1/e$に特異点をもつため、$x\to 1/e$での漸近挙動が一致する標準的な関数$g(x)$を探した。その結果、$g(x)=\displaystyle{\frac{1}{\sqrt{2}\sqrt{1-ex}}}$を発見した。
3. $g(x)$を通常型母関数にもつ数列$g_n$の漸近挙動が$\displaystyle{g_n \sim \frac{e^n}{\sqrt{2\pi n}}}$であることを求めた。
4. $f_n$の漸近挙動と$n!g_n$の漸近挙動は一致するので、$f_n$の漸近挙動が$\displaystyle{f_n \sim \frac{n! e^n}{\sqrt{2\pi n}}}$であることがわかった。

数列の世界で「$n\to\infty$での漸近挙動が同じ」ものどうしが、母関数の世界では「特異点まわりでの漸近挙動が同じ」ものどうしである、というシンプルな対応がとてもきれいです。せっかくですから、頭を整理するためにもここで用いた事実を定理としてまとめておきましょう。

すごい定理

関数$f(x)$およびある実数$x_0$に対して

$$ f(x)\sim \frac{C}{\displaystyle{\sqrt{1-\frac{x}{x_0}}}}\; (x\to x_0) $$

が成り立つならば、$f(x)$を母関数にもつ数列$f_n$は

$$ f_n\sim \frac{C}{x_0^n\sqrt{\pi n}}\; (n\to\infty) $$

を満たす。ただし$C$は定数である。

この定理において$x_0=1/e, C=1/\sqrt{2}$としてみると、ちょうど今までやってきたことに対応します。

ところで、ついさっき求めた

$$ n^n \sim \frac{n! e^n}{\sqrt{2\pi n}} \; (n\to\infty) $$

はスターリングの公式（Stirling's formula）と呼ばれる有名な式です。この式は、おもに階乗$n!$の$n\to\infty$での漸近挙動を求めるために使われ、これを変形した

$$ n! \sim\sqrt{2\pi n}\left(\frac{n}{e}\right)^n \; (n\to\infty) $$

という形でお目にかかることが多いです。

ラストスパート

数列$n^n$で感覚をつかんだところで、最終目標である

$$ \sum_{k=0}^n {}_n{\rm C}_k k^n $$

の漸近挙動を求める準備が整いました。いよいよ本番ですよ！

むっちゃドキドキしてきた…。

皆さん、今日くらいは休んで明日に備えますよね？

……………。

いやファボゼロのボケすんな！

はい。というわけで始めていきましょう。出発点となるのは、この数列の指数型母関数である

$$ \frac{1}{1+W(-xe^x)} $$

です。この関数は$x=W(1/e)=w$に特異点をもつので、$x\to w$での漸近挙動が同じ関数を発見してやりましょう。

そのときに活躍するのが、さっき求めた

$$ \frac{1}{1+W(-y)}\sim\frac{1}{\sqrt{2}\sqrt{1-ey}} \; \left(y\to \frac{1}{e}\right) $$

という式*12。2つの式を比較すると、これに$y=xe^x$を代入すればいいことがありそうです。

$$ \frac{1}{1+W(-xe^x)}\sim\frac{1}{\sqrt{2}\sqrt{1-xe^{x+1}}} \; \left(x\to w\right) $$

はい、こんな感じです（$x\to w$のとき$y=xe^x \to 1/e$になるので、きちんと辻褄が合っています*13）。

というわけで、$x\to w$での漸近挙動が同じになる

$$ \frac{1}{\sqrt{2}\sqrt{1-xe^{x+1}}} $$

という関数を発見しました。とはいえ、このままでは関数の形が複雑で都合が悪いので、さらに変形をしていきましょう。ルートの中身である$1-xe^{x+1}$を$x=w$のまわりで$1$次の項までテイラー展開してやります。結果はこちら。

$$ 1-xe^{x+1}=(1+e^{1+w})(w-x)+O( (x-w)^2 ) $$

WolframAlphaにSeries[1-xe^(x+1), {x, ProductLog[1/e], 1}]と入力すれば一瞬で出ますが、頼りすぎはいけません。普通に$1-xe^{x+1}$を1回微分して$x=w$を代入すれば$1+e^{1+w}$という値が出てきます。ちなみに僕は怠惰なのでWolframAlphaを使いました。

さて、この結果を用いれば

$$ \frac{1}{1+W(-xe^x)}\sim\frac{1}{\sqrt{2}\sqrt{1-xe^{x+1}}}\sim\frac{1}{\sqrt{2(1+e^{1+w})}\sqrt{w-x}} \; \left(x\to w\right) $$

が分かります。こうして、$x\to w$での漸近挙動が同じになる「単純」な関数

$$ \frac{1}{\sqrt{2(1+e^{1+w})}\sqrt{w-x}} $$

が見つかりました！ この関数は、形としては$\displaystyle{\frac{1}{\sqrt{1-x}}}$型に分類されるので、さっきの定理の結果を利用することができます。これはもう勝ちましたね。

定理の形に当てはめるために

$$ \frac{1}{\sqrt{2(1+e^{1+w})}\sqrt{w-x}}=\frac{1}{\sqrt{2w(1+e^{1+w})}\displaystyle{\sqrt{1-\frac{x}{w}}}}=\frac{1}{\sqrt{2(1+w)}\displaystyle{\sqrt{1-\frac{x}{w}}}} $$

と変形します。最後の等式では、$we^w=1/e$であることを利用して

$$ w(1+e^{1+w})=w+we^{1+w}=w+we^w\cdot e=w+\frac{1}{e}\cdot e=1+w $$

という変形を行いました。あとは

$$ x_0=w, C=\frac{1}{\sqrt{2(1+w)}} $$

として定理を適用するだけです。$\displaystyle{\frac{1}{1+W(-xe^x)}}$が「指数型」母関数であることに注意して$n!$を忘れなければ

$$ \sum_{k=0}^n {}_n{\rm C}_k k^n\sim \frac{n!}{w^n \sqrt{2\pi n(1+w)}} \; (n\to\infty) $$

という式を得ます。

あとはもうひと踏ん張りです。さっき導出したスターリングの公式

$$ n! \sim\sqrt{2\pi n}\left(\frac{n}{e}\right)^n \; (n\to\infty) $$

を用いて$n!$を消去します。すると……？

$$ \sum_{k=0}^n {}_n{\rm C}_k k^n \sim \frac{1}{\sqrt{1+w}}\left(\frac{n}{ew}\right)^n \; (n\to\infty) $$

お！

おおおお！！！！！！

おおおおおおおおお！！！！

おおおおおおおおおおおおおおおおおううううううううぅぅぅぅぅぅぅsdくfgdしfじゃwfゔぇいうwfhwfhwfうあえsgつwdgづy！！！！！！！！！（語彙力）

できた！ できました！ 「二項係数を含む和で表された数列」という単純なつくりのものから、ランベルトのW関数が現れるのを見届け、そして漸近挙動を解き明かしていく過程を、（端折ったところはあるものの）すべて追うことができました……！

おわりに

というわけで、とある数列を題材に、さまざまな手法を用いてその性質を探る旅のもようをお送りしてきましたが、皆さんいかがでしたか。数列の母関数、漸近挙動、それを解析的な手法を用いて調べる方法。これらはおそらく、中学、高校、大学初年度で学ぶ数学にはあまり登場しない話題でしょう。高校数学の花形は微分積分でしょうし*14、今回紹介した組合せ論という分野はどちらかといえばマイナーな部類に入ると思います。だからこそ、今回はそういうニッチな分野の数学に触れることができてとても新鮮でした。一見単純で研究し尽くされたようなトピックであっても、ちょっと脇道に入ると、そこには豊かな数学の謎が広がっているんだなあ、ということを感じました。

また、今回紹介した証明は、完全に自力で到達したわけでは決してありません。インターネット上に転がっているたくさんの資料や、WolframAlphaやDesmosなどのWebアプリケーションの力を借りて始めてできたことです。いわば、巨人の肩から肩へとぴょんぴょん飛び移りまくったわけですが、それだけでもめちゃくちゃ達成感があります。地道に文献を探すのは骨が折れますが、様々な論文や書籍の記述をもとに証明の道筋を完成させたときの喜びはひとしおです。

この記事を通して、数学で遊ぶ楽しさのようなものを少しでも感じていただければ幸いです。

最後に、この問題を僕のところに持ち込んできてくれ、一緒に証明を考えてくれた友人に感謝します。

それではまた次の記事で会いましょう。さようなら。

参考文献

[1] Corless, R. M., Gonnet, G. H., Hare, D. E., Jeffrey, D. J., & Knuth, D. E. (1996). On the LambertW function. Advances in Computational mathematics, 5(1), 329-359.
[2] Knuth, D. E., & Pittel, B. (1989). A recurrence related to trees. Proceedings of the American Mathematical Society, 105(2), 335-349.
[3] Riordan, J. (1968). Combinatorial identities., Wiley, New York.
[4] Gessel, I. M. (2016). Lagrange inversion. Journal of Combinatorial Theory, Series A, 144, 212-249.
[5] Harris, B., & Schoenfeld, L. (1967). The number of idempotent elements in symmetric semigroups. Journal of Combinatorial Theory, 3(2), 122-135.
[6] Comtet, L. (2012). Advanced Combinatorics: The art of finite and infinite expansions. Springer Science & Business Media.
[7] Flajolet, P., & Sedgewick, R. (2009). Analytic Combinatorics. cambridge University press.

*1:ProductLog[x]はランベルトのW関数のことです。

*2:この定理には等価な表現が複数あることに注意してください。

*3:簡単に言えば、複素数の範囲での微分積分を考える分野のことです。

*4:すなわち、関数$\displaystyle{\frac{1}{1+W(-xe^x)}}$は$\displaystyle{\frac{1}{1+W(-x)}}$と$xe^x$の合成関数になっているということです。

*5:過激派「$e^x$のべき級数展開ぐらい生まれたときから知ってろ」

*6:各因数の次数は少なくとも$1$あるので、$x^{N-k+1}$より次数の大きい項をとってくることはできません。掛け合わせた結果が$x^N$を超えてしまいます。

*7:ここで紹介したのは、べき級数で表された関数を合成したときに、合成後の関数のべき級数展開を求めるための最も一般的な手法です。その方法を一般的に書き表した公式はFaà di Bruno's formulaと呼ばれています。

*8:余談ですが、$\displaystyle{\sum_{k=0}^n{}_n{\rm C}_k k^{n-k}}$は冪等数（idempotent number）と呼ばれる数列で、$n$個の元からなる集合から自分自身への写像のうち、冪等写像であるものの総数を表します（OEIS:A000248を参照）。ここで$f$が冪等写像であるとは、$f^2=f$が成り立つことをいいます。

*9:二項係数${}_n{\rm C}_r$は通常$n,r$が$0\leq r\leq n$なる自然数であるときに定義されますが、それを拡張して、$n$が一般の実数のときにも$\binom{n}{r}=n(n-1)\cdots (n-r+1)/r!$でもって二項係数を定義することができます。これを一般化二項係数といいます。

*10:証明は文献[7] (Flajolet & Sedgewick, 2009)のp.381-383などを参照してください。

*11:$f(x)$が$f_n$の「指数型」母関数であるのに対し、$g(x)$は$g_n$の「通常型」母関数です。$n!$のファクターを忘れないでください。

*12:説明が分かりやすくなるように、変数を$x$から$y$に変えています。

*13:よく考えたら合成関数なんだから#それはそうでした。

*14:異論は認めます。

二項係数にからんだ数列の極限を考えようとしたら闇が深かった話（前編）

突然ですが、みなさん二項係数は好きですか？ 僕は普通です。

最近、友人と二項係数についての問題を考えていたので、その顛末を簡単に書いてみようかなと思います。

梅雨がやっと明けたばかりの7月のことでした。所属しているサークルの集まりに久しぶりに顔を出したら、数学好きの友人がノートPCを抱えて僕のところに近づいてきます。話を聞いてみると、最近とある数列のことを考えていて夜も眠れないらしい（大意）。その日は偶然にも暇だったので、ちょっと面白そうかもしれないと思って一緒に考えてみることにしました。

とある数列

その数列というのは次のようなものです。

$$ 1, 1, 6, 54, 680, 11000, 217392, 5076400, 136761984, \cdots $$

いきなり何桁もの数字の羅列を見せられて「は？」という感じですが、これは第項が

$$ \displaystyle{\sum_{k=0}^n {}_n{\rm C}_k k^n} $$

で与えられる数列です。え？なんでこんな数列を考えようと思ったかって？ そんなの知りません。彼に聞いてください。

とにかく、こういう和の形で表された数列があったとき、まずは一般項を和の記号を使わないで表してみたくなりますよね。 そうはいっても、シグマ記号の中に二項係数${}_n{\rm C}_k$が入っているので、一筋縄では表せそうにありません。

シグマ記号の中がもっと簡単な式だったら、一般項をシグマ記号を使わないで表すことができることもあります。例えば

$$ \displaystyle{\sum_{k=0}^n {}_n{\rm C}_k}=2^n $$

という式が有名です。証明もそんなに難しくはありません。を二項定理で展開すれば

$$ 2^n=(1+1)^n=\sum_{k=0}^n {}_n{\rm C}_k 1^k1^{n-k}=\sum_{k=0}^n {}_n{\rm C}_k $$

となりますから上式が得られます。ちなみにこの式に$n=0$を代入するとさっきの数列の初項になったりします（よく考えたらそれはそう）。

実は、この式をもとにすると二項係数の入った和の式を大量に生産することができます。突然ですが、$(1+x)^n$という多項式を二項定理を使って展開すると

$$ (1+x)^n=\sum_{k=0}^n {}_n{\rm C}_k x^k $$

となります（さっき登場した式は、この式に$x=1$を代入すると得られる式ですね）。

ここからどうやって新しい式を得るかというと、両辺を$x$で微分するんです。 すると、右辺についてはシグマ記号の各項を微分すればいいので

$$ n(1+x)^{n-1}=\sum_{k=0}^n {}_n{\rm C}_k {kx}^{k - 1} $$

となります。これに$x=1$を代入すれば

$$ n\cdot 2^{n-1}=\sum_{k=0}^n {}_n{\rm C}_k k $$

という式のできあがり。もう気づいている人もいるかもしれませんがこの式に$n=1$を代入したものは、例の数列の第1項（2番目の項）そのものです。

今やった計算は何回も繰り返すことができます。ただし注意が必要で、さっきの式の両辺を何も考えず$x$で微分してしまうとシグマの中身が$k(k - 1)$となってしまうので、先に両辺に$x$を掛けて

$$ nx(1+x)^{n-1}=\sum_{k=0}^n {}_n{\rm C}_k {kx}^{k} $$

としてから$x$で微分します。

$$ n(1+x)^{n-1}+n(n-1)x(1+x)^{n-2}=\sum_{k=0}^n {}_n{\rm C}_k {k^2x}^{k - 1} $$

はい微分しました（ちょっと大変だけど）。これに$x=1$を代入すると

$$ n(n+1)\cdot 2^{n-2}=\sum_{k=0}^n {}_n{\rm C}_k {k^2} $$

が得られます。慧眼な読者はもう気づいているでしょうが$n=2$を代入すると

$$ \sum_{k=0}^2 {}_2{\rm C}_k {k^2}=2\cdot 3=6 $$

ですがこれはさっきの数列の第2項になっています。

先ほども言ったように、この計算は何回でも繰り返すことができます。とはいえ微分の計算がちょっと大変です。$nx(1+x)^{n-1}+n(n-1)x^2(1+x)^{n-2}$なんて見るからに微分したくないですよね。こういう時はWolframAlphaくんに助けてもらうのがいちばんです。

というわけで今の計算を繰り返すと

$$ \sum_{k=0}^n {}_n{\rm C}_k {k^3}=n(n^2+3n)\cdot 2^{n-3} $$

$$ \sum_{k=0}^n {}_n{\rm C}_k {k^4}=n(n^3+6n^2+3n - 2)\cdot 2^{n-4} $$

$$ \sum_{k=0}^n {}_n{\rm C}_k {k^5}=n(n^4+10n^3+15n^2 - 10n)\cdot 2^{n-5} $$

わあすごいですね。繰り返しますが、この式にそれぞれ$n=3, 4, 5$を代入すると例の数列の第3項、第4項、第5項になります。

ここまで偉そうに説明してきましたが、この導出は全部友人が考えたものです。僕が「え〜何これすごい！」と言うと彼は「これくらい普通の人間なら考えつくでしょ」とか言ってイキってきました。ちょっと何言ってるかわかんないですね。

そういえば一般項を求めようとしていた

ここまでの話を整理しておきましょう。何をしていたかというと、

$$ 1, 1, 6, 54, 680, 11000, 217392, 5076400, 136761984, \cdots $$

という例の数列の一般項を、シグマ記号を使わない形で求めようとしていたんでした。とはいえ、それを求めるのはかなり難しそうです。さっき分かったのは、「この数列の第$n$項を知りたかったら、

$$ \sum_{k=0}^n {}_n{\rm C}_k k=n\cdot 2^{n-1} $$

$$ \sum_{k=0}^n {}_n{\rm C}_k {k^2}=n(n+1)\cdot 2^{n-2} $$

$$ \sum_{k=0}^n {}_n{\rm C}_k {k^3}=n(n^2+3n)\cdot 2^{n-3} $$

$$ \sum_{k=0}^n {}_n{\rm C}_k {k^4}=n(n^3+6n^2+3n - 2)\cdot 2^{n-4} $$

$$ \sum_{k=0}^n {}_n{\rm C}_k {k^5}=n(n^4+10n^3+15n^2 - 10n)\cdot 2^{n-5} $$

という式の$n$番目に$n$を代入しなさいね」ということであって、数列の一般項がひとつの式で表されたわけではありません。

いやー、困った困った。でもなんとかしてこの数列のことをもっとよく知りたいですよね。もう一度、数の並びを見てみましょう。

$$ 1, 1, 6, 54, 680, 11000, 217392, 5076400, 136761984, \cdots $$

改めて見てやると、数がものすごい勢いで増えていっています。第4項までは$1,1,6,54,680$と地に足がついている感じなのに（0番目から数えています）、第5項でいきなり$11000$ですからね。いきなりどうした？って感じです。

こんなに増加するスピードが速いと、ほかの数列と増え方を比べたくなってきます。

増加するのがとても速い数列の代表といえば、階乗$n!$があります。さっきの数列と同じ項数だけ取り出すとどうなるのか見てみましょう。

$$ 1, 1, 2, 6, 24, 120, 720, 5040, 40320, \cdots $$

この数列の第8項、すなわち$8!$が$40320$であるのに対し、例の数列の第8項は$136761984$ですから、4桁も違うことが分かります。でも、単に両者を比べてみてもちょっと分かりにくいですね。

そんなときには、2つの数列の比をとってみると分かりやすいです。つまり、$a_n=\displaystyle{\sum_{k=0}^n {}_n{\rm C}_k k^n},\; b_n=n!$として、$a_n/b_n$の値を調べるわけです。こうすれば、例の数列が階乗の何倍なのかがわかります。 $n$を大きくしていったとき、比の値が$1$に近づけば、両者の増え方は同程度だと見なすことができます。また、比の値が限りなく大きくなるのなら、例の数列の増加スピードが階乗よりも桁違いに大きいことがわかりますし、比の値が$0$に近づくなら、階乗の増加スピードのほうが速いことが分かりますね*1。やってみましょう。

$$ 1,1,3,9, 28, 92, 302, 1007, 3392, \cdots $$

このようになりました（※値は四捨五入して整数にしています）。見るからに、比の値は増加し続けていますね。これは、例の数列の増加スピードが階乗よりも速いことを意味しています。まあ両者を見比べた時点でそんな感じはしていました。

同じスピードで増える数列を探せ

さて、例の数列が階乗を超えるスピードで増加することがわかりました。ここまでくると、例の数列の増加スピードが正確にどれくらいなのか知りたくなってきます。 でも、未知の数列が増加するスピードなんてどうやって求めるのでしょう？　それは、「我々のよく知っている数列で、例の数列と同程度のスピードで増加するものを見つければいい」んです。仮にですよ、$c_n$という具体的な数列があって、$c_n$の増加スピードが例の数列と同じなら、例の数列の増加スピードが分かるわけです。そのような$c_n$を見つけることを、数学では「数列の漸近挙動を調べる」とか言ったりします。そして、$c_n$を見つけるには、例の数列との比をとって、$n$を大きくしたときに$1$になるものを探せばいい。話だけなら単純です。

でもその$c_n$ってどうやって見つければよいのでしょう？　とりあえず、例の数列が階乗よりも増加スピードが速いことだけは分かったので、少なくとも$c_n$は階乗よりも速く増加する人々の中から探せばよいでしょう。それでも、階乗よりも速く増加する数列なんて無数にあります。

ここで、前に導出した式に戻りましょう。これです。

$$ \sum_{k=0}^n {}_n{\rm C}_k k=n\cdot 2^{n-1} $$

$$ \sum_{k=0}^n {}_n{\rm C}_k {k^2}=n(n+1)\cdot 2^{n-2} $$

$$ \sum_{k=0}^n {}_n{\rm C}_k {k^3}=n(n^2+3n)\cdot 2^{n-3} $$

$$ \sum_{k=0}^n {}_n{\rm C}_k {k^4}=n(n^3+6n^2+3n - 2)\cdot 2^{n-4} $$

例の数列$a_n$の各項は、これらの式に、$n=1,2,3,\cdots$を順番に代入すれば出てくるのでした。代入してみましょう。

$$ a_1=\sum_{k=0}^1 {}_1{\rm C}_k k=1\cdot 2^{1-1}=1 $$

$$ a_2=\sum_{k=0}^2 {}_2{\rm C}_k {k^2}=2\cdot (2+1)\cdot 2^{2-2}=2^2+2=6 $$

$$ a_3=\sum_{k=0}^3 {}_3{\rm C}_k {k^3}=3\cdot (3^2+3\cdot 3)\cdot 2^{3-3}=3^3+3\cdot 3^2=54 $$

$$ a_4=\sum_{k=0}^4 {}_4{\rm C}_k {k^4}=4\cdot (4^3+6\cdot 4^2+3\cdot 4 - 2)\cdot 2^{4-4}=4^4+6\cdot 4^3+3\cdot 4^2-2\cdot 4=680 $$

よく見てください。$a_2$には$2^2$という項があります。次の$a_3$には、$3^3$という項があります。そして、$a_4$には$4^4$が登場しています。このままいくと、$a_n$には$n^n$という項が現れそうです*2。

ということは、まず手始めに、$a_n$と同程度で増える数列$c_n$の候補として$n^n$をとってくればよさそうです*3。参考までに、$n^n$の各項を並べてみると

$$ 1, 4, 27, 256, 3125, 46656, 823543, 16777216, 387420489, \cdots $$

うん、さっきよりは期待できそう。さっそく比をとってみましょう。$a_n/c_n$を計算します。

$$ 1, 1, 1.5, 2, 2.7, 3.5, 4.7, 6.2, 8.2, \cdots $$

こんな感じになりました（※値は小数第2位を四捨五入しています）。うーん、どんどん増加していって、$1$にはならなそうです。 それでも、階乗のときと比べると、増加の仕方はだいぶ穏やかですね。比の値の変化の仕方にも秘密がありそうです。

こんなときはDesmosを使いましょう。Desmosは数学徒御用達の万能視覚化ツールで、座標平面上にさまざまなグラフを描くことができます。想像以上に高機能で、関数のグラフはもちろん、パラメータ表示された曲線を描いたり、点を動かしたりすることもできます。

これがDesmosの画面です。いまからここに点をプロットしていきましょう。まずは横軸を$n$、縦軸を例の数列$a_n$にとって、第$10$項まで表示させてみます。

はいできました。一瞬です。とはいえ、この数列はありえないほどのスピードで増えるので、縦軸の目盛りをありえないほど細かくしても最初の数項しか見えていません。

気を取り直して$n^n$もプロットしましょう。$n=0, 1, \cdots, 10$に対して点$(n, n^n)$を表示させます。

なんかおしいことはわかるけどよくわからん。そこで、両者の比の値をプロットしてみます。

わあ！ なんか見たことのある曲線がでてきた！ 僕知ってます、知ってますよ。これ指数関数ってやつでしょ。いや数列だから等比数列か。この紫の点列、何かの等比数列$ar^n$と重ねてみると$n$が大きいところではほとんどぴったり一致しそうじゃないですか。

紫の点が等比数列っぽい増え方をするなら、公比$r$があるはずです。

公比、知りたい…。知りたくない…？

僕は知りたいので、とりあえず

$$ 1, 1, 1.5, 2, 2.7, 3.5, 4.7, 6.2, 8.2, \cdots $$

の隣同士の比をとって見ましょう。それが近づいていく先が求めたい公比$r$です。

$n$	$a_n$	$n^n$	$r_n=a_n/n^n$	$r_n/r_{n-1}$
0	1	1	1.00000
1	1	1	1.00000	1.00000
2	6	4	1.50000	1.50000
3	54	27	2.00000	1.33333
4	680	256	2.65625	1.32812
5	11000	3125	3.52000	1.32517
6	217392	46656	4.65946	1.32371
7	5076400	823543	6.16409	1.32291
8	136761984	16777216	8.15164	1.32243
9	4175432064	387420489	10.77751	1.32212

いちばん右の列に注目してください。なんかめっちゃ$1.32\cdots$に近づいていってませんか？ もしかしてこれが公比$r$なのではないでしょうか？

公比$r$のおおまかな値は、Desmosを利用しても求めることができます。順を追って説明しますね。

まずは、縦軸を対数目盛りにします。どういうことかというと、$(n, a_n/n^n)$をプロットするかわりに$(n, \log{(a_n/n^n)})$をプロットするということです。あ、Desmosでは自然対数は$\log$ではなく$\ln$で書くので気をつけてくださいね。すると…

めっちゃ直線上に並んでるー！ 実は、等比数列$ar^n$を、縦軸を対数目盛りにしてプロットすると点は直線に並ぶのです。理由は簡単。横軸に$n$、縦軸に$\log(ar^n)$をプロットしたのですから、$x$と$y$の関係は

$$ y=\log(ar^x) $$

になっているはずです。右辺を対数の性質を使って変形してやると

$$ y=(\log{r})x+\log{a} $$

となり、これは傾きが$\log{r}$で切片が$\log{a}$の直線を表しています。だから、縦軸を対数目盛りにして等比数列をプロットすると、点が直線に並ぶわけです。

ということはですよ、直線に並んだ紫の点の傾きを求めてやれば、公比$r$が求められるのでは…？ 傾きが$p=\log{r}$なのですから、傾き$p$から$r$を求めるには$r=e^p$を計算すればいいわけです*4。

さっそく傾き（の近似値）を求めましょう。直線からのずれが少ない、$n$が大きい部分の2点を代表して選び、2点間の傾きを計算します。

計算しやすいように$(5, 1.258)$と$(15,4.051)$の2点を選びました。そこから傾き$p$を求めると

$$ p\simeq\frac{4.051-1.258}{15-5}\simeq 0.2793 $$

となり、この$p$の値から算出される公比$r$は

$$ r=e^p \simeq e^{0.2793}=1.322\cdots $$

になります。やっぱり$1.32\cdots$という値が出てきました。

ここまでわかったこと

ここで少し、今までの話を整理しましょう。

$$ a_n=\sum_{k=0}^n {}_n{\rm C}_k k^n $$

という数列の増加スピードを調べていました。目標は、$a_n$と同程度に増える数列$c_n$を見つけること、すなわち$a_n/c_n$の値が$n\to\infty$のとき$1$に収束するような数列$c_n$を見つけることです。いちいち「同程度に増える」とか「比の値が$n\to\infty$のとき$1$に収束する」とか言っていると面倒なので、このことを

$$ a_n\sim c_n $$

という記号で表すことにしましょう。現在の目標は、

$$ \sum_{k=0}^n {}_n{\rm C}_k k^n \sim c_n $$

になるような数列$c_n$を発見することです。そこで、$a_n$という数列を$n^n$で割ったものを考えたのですが、これが等比数列$ar^n$っぽい増え方をするようなのでした。先ほどの記号で書けば

$$ \frac{a_n}{n^n}\sim ar^n $$

ということです。言い換えると

$$ a_n=\sum_{k=0}^n {}_n{\rm C}_k k^n \sim ar^nn^n $$

ですね。ここで注意ですが、この式はあくまで予想であって、まだ証明したわけではありません。

この式において、定数$a$も$r$も未知ですが、先ほどの考察から、$r$がおよそ$1.32$であることが分かりました。

1.32の正体を探す

ここまでくると、俄然$a$や$r$が何なのか知りたくなりますね。$a$と$r$が分かれば、$a_n$と同程度に増える数列がまさに見つかるわけです。特に$r$については、$1.322$という近似値まで分かっていますから、あとはこれが何の近似値なのか分かればいいのです。

さて、皆さんはWolframAlphaにすごい機能があるのを知っていますか？ WolframAlphaの検索窓に、$1.322$と入力してみてください。

はい。入力しましたか？ よろしい。そうしたら、検索結果を下にスクロールしください。

なんと、WolframAlphaくんは有能なので、$1.322$を入力すると$1.322$を近似値にもつような実数の候補を教えてくれるんです。控えめに言って天才です。勝てへん。

1段目に出てくる$\displaystyle{\frac{\pi\log\pi}{e}}$はまだわかります。2段目に出てくる$\displaystyle{-\frac{2H_4}{5}}$に至ってはもはや意味がわかりません。「4th hundred-dollar challenge constant」って何ですか。Wikipediaによると、

$$ \exp\sin{50x}+\sin{60e^y}+\sin(70\sin x)+\sin(\sin 80y)-\sin 10(x+y)+(x^2+y^2)/4 $$

という関数の最小値を$H_4$というらしいですが、何でこんな関数の最小値に名前をつけようと思ったんでしょうか。謎です。

さて、WolframAlphaくんに$1.322$の正体の候補を出してもらいました。$\displaystyle{\frac{\pi\log\pi}{e}}$なんてめちゃめちゃそれっぽいですよね。もうこれでいいじゃん。あとは証明するだけ。

…そう思って証明をつけようと頑張りましたが、いくらやってもできませんでした。友人と僕の数学力が足りないのか、予想が外れているのか、どちらなのかは分かりませんが、たぶん両方だと思います。

オンライン整数列大辞典とかいうのがすごい

ところで、世の中にはオンライン整数列大辞典(OEIS)というものがあります。これです。

オンライン整数列大辞典は、古今東西ありとあらゆる数列を集めたインターネット上の大辞典です。そこに、例の数列を入力してみます。

すると…

まさにこの数列の記事が載っとる

や
ξ
ん

……載ってました。

オンライン整数列大辞典に収録されている数列には、識別番号がついています。どうやら、この数列の識別番号はA072034のようですね。

さて、この大辞典には数列ごとに個別のページがあり、そこにたくさんの有益情報が載っています。A072034もその例に漏れず、何やら色々かいてあります。COMMENTSという欄にはこの数列の特徴付け（具体的意味）が書いてあったりします。なになに？

COMMENTS: The number of functions from {1,2,...,n} into a subset of {1,2,...,n} summed over all subsets.

要するに、$\displaystyle{\sum_{k=0}^n {}_n{\rm C}_k k^n}$というのは「$n$個の元からなる集合を定義域とし、その部分集合を値域とする写像の総数（ただし対応としては同じ写像でも値域が違うものは区別する）」を意味しているらしいです。よく考えればたしかにそうだ。

その下にあるFORMULAという欄には、数列の一般項の別表現だったり、母関数だったり、漸近挙動だったりといったお役立ち情報が載っています。なるほど。じゃあこの数列のFORMULA欄も見てみようか。

ん？？

？？？

！？！？！？！？

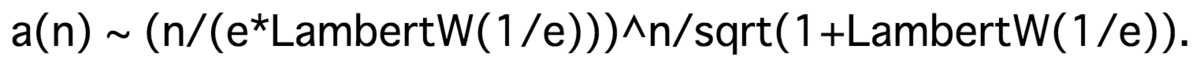
何ですかこれ。どこから降ってきたんですか。ありえんゴツくないですかこれ。てかLambertWって何だよ。

LambertWというのはランベルトのW関数のことです。僕も数学徒の端くれなのでランベルトのW関数のことは定義だけ知っていました。関数$f(x)=xe^x$の逆関数のことをランベルトのW関数といい、$W(x)$と書きます。つまり$y=W(x)$とは

$$ x=ye^y $$

と同じことを言っているということです。お察しの通り、$W(x)$を三角関数や指数関数といった初等関数の組み合わせで表現することはできません。いわゆる特殊関数というやつです。

さて、この式を見るに、$W(1/e)$なる数を使えば、どうやらこの数列A072034と同じスピードで増加する数列を表現できるらしいのです。定義から、$W(1/e)$というのは

$$ xe^x=\frac{1}{e} $$

を満たす実数のことですね。WolframAlphaによれば、その値はおよそ$0.278$だそう。

そして、オンライン整数列大辞典さまによると、実は

$$ a_n=\sum_{k=0}^n {}_n{\rm C}_k k^n \sim \frac{1}{\sqrt{1+w}}\left(\frac{n}{ew}\right)^n $$

が成り立っているらしい（$w=W(1/e)=0.278\cdots$）。はたして本当にそうでしょうか。

でも、この式は、さっきDesmosとにらめっこしながら予想した

$$ a_n=\sum_{k=0}^n {}_n{\rm C}_k k^n \sim ar^nn^n $$

と形の上では一致しています。なぜなら、この式において

$$ a=\frac{1}{\sqrt{1+w}}, \; r=\frac{1}{ew} $$

とすれば、まさに辞典に載っている式になるからです。極め付けは、

$$ \frac{1}{ew}=1.321\cdots $$

になることです。WolframAlphaくんがそう言っています。

紫の点の傾きから算出した$1.32$という値が登場しました。どうやら

$$ a_n=\sum_{k=0}^n {}_n{\rm C}_k k^n \sim \frac{1}{\sqrt{1+w}}\left(\frac{n}{ew}\right)^n $$

が成り立っている可能性はかなり高いようです。

それにしてもやばい式ですよね。どこからランベルトのW関数が出てくるのかまったく想像がつきません。

証明したい

こんな式を見せられたら、証明したくなるのが人情というものです。ん？ 証明したくならない？ そういう数学に興味ないやつ大学生活心配なんだよね。ちゃんと人とコミュニケーションとれてる？ え？ ３人で歩いてると気づいたら自分以外の２人が前を歩いててその後ろを無言でついていきがち？

じゃあ俺と一緒だね()

………はい。

というわけで、式自体はオンライン整数列大辞典とかいうチートを使って超自然的に発見してしまったので、証明ぐらいは自力でやり遂げたいですね。実は先日、数々の偶然が重なって証明をつけることに成功したのですが、長くなったので続きは後日書きたいと思います。

それではこの辺で。さようなら。

後編はこちらから↓

halphy.hatenablog.com

*1:比の値が$1$または$0$以外の定数に近づく場合もありますが、これは両者の増え方は同程度だが定数倍の差があるということを意味します。

*2:実際にこれは成り立ちます。

*3:ただし、これは$a_n$が$n^n$の程度で増えることを必ずしも意味しません。あとで見るように、実際そうなっていません。

*4:さらに、この点列にいちばんよくフィットする直線を求めて、その切片が分かれば$a$の値も分かります